燕尾模型的主要结论及应用
燕尾模型的基础是等高三角形面积比等于对应底边之比(图1)。
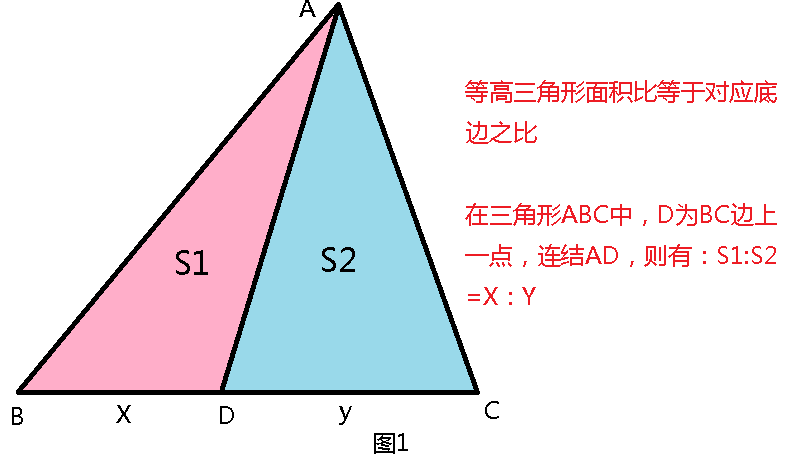
在三角形 ABC中, D为BC上一点,连接AD;取AD上点O,连接OB、OC,则有图2中的面积和线段比例关系,即燕尾模型公式。
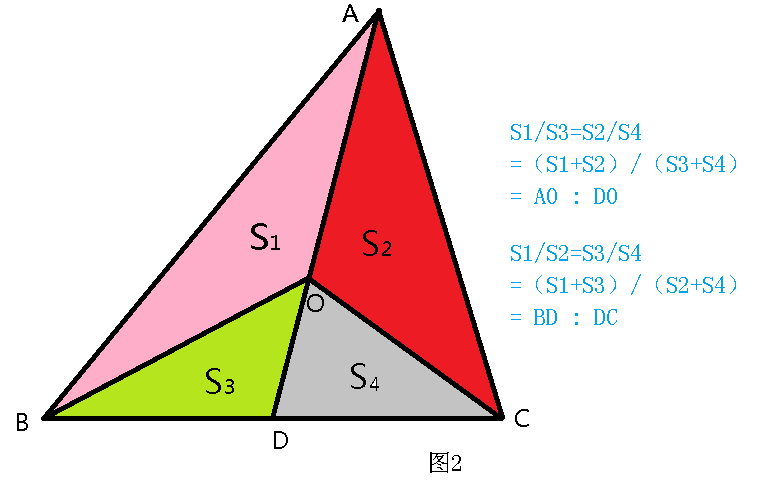
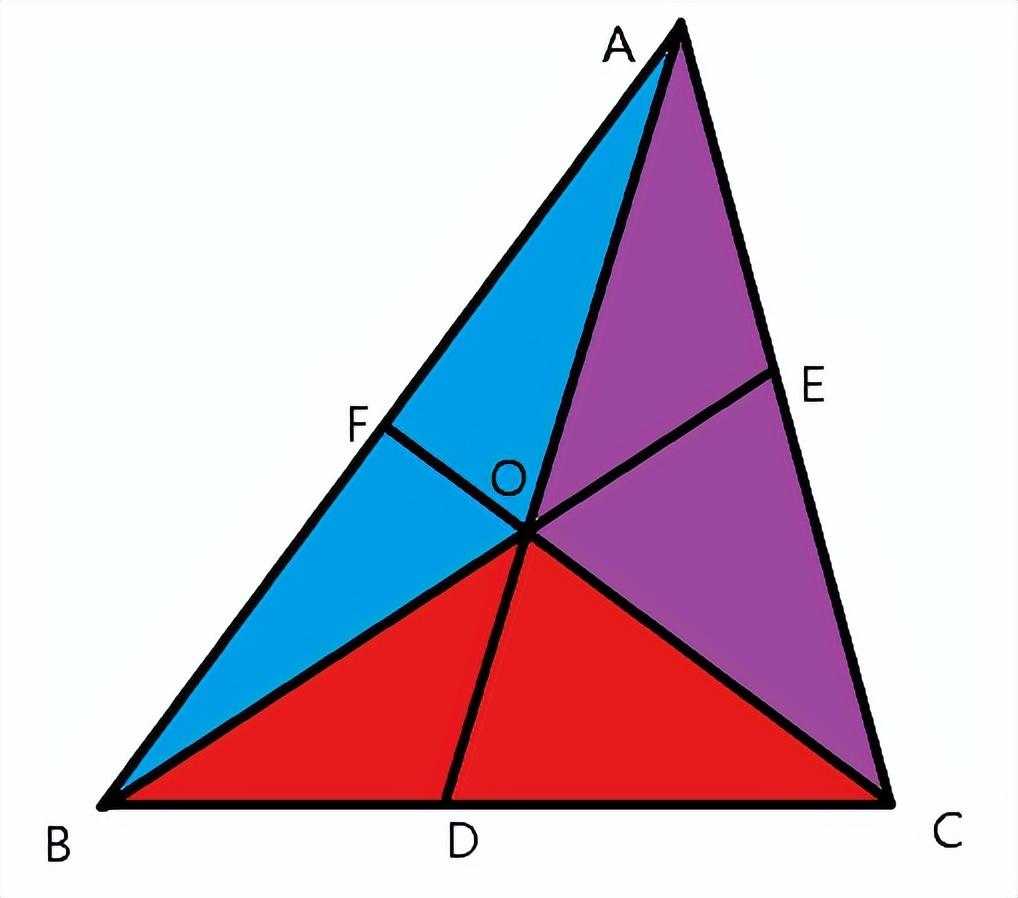
如果将图2中的BO、CO延长分别交AC于E和AB于F,根据燕尾模型公式及比例性质可得到如图3中的面积比和线段比的等量关系。
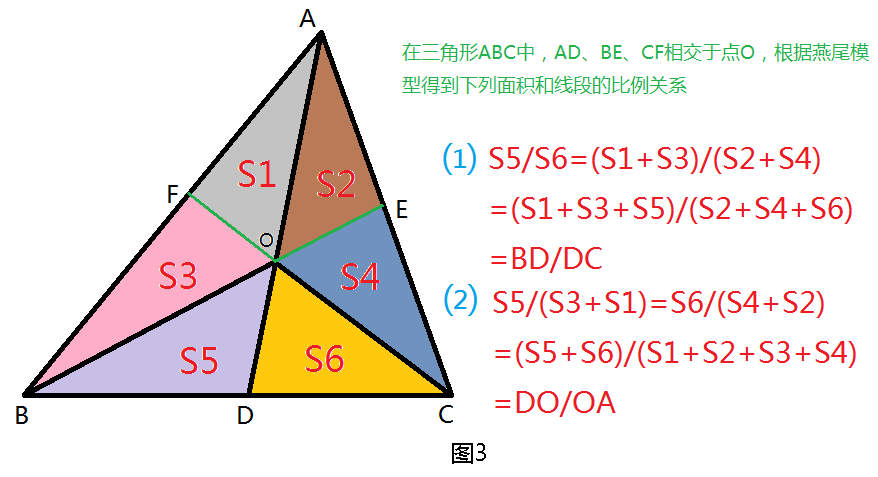
燕尾定理因此图形类似燕尾而得名,是一个关于三角形的基础定理,在许多几何题目中有着广泛的运用,为三角形面积与对应底边之间建立了等量关系,现举例如下。
题目1:如图,在△ABC中,点D、E、F分别在边BC、AC、AB上,AD、BE、CF相交于点O,若BD/DC=2/3,AE/CE=5/3,则AF/BF的值为(5/2)。
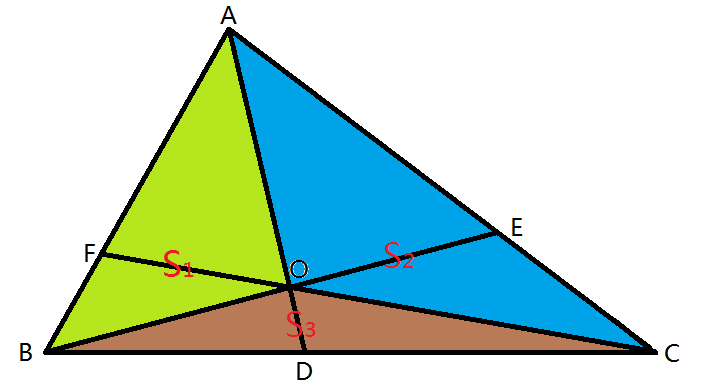
解题思路:根据燕尾模型公式,先将已知线段比转化为面积比,进行简单运算后再将面积比转化为线段比。
将S△AOB、S△AOC、S△BOC分别标识为S₁、S ₂和S ₃。根据燕尾模型公式得:
S₁/ S ₂= BD/DC=2/3…………①;
S₁/ S ₃ = AE/CE=5/3…………②。
将②/①得:
S₁/ S ₃·S ₂/ S₁=5/2,
S ₂/ S ₃=5/2。
故AF/BF= S ₂/ S ₃=5/2。
题目2:如图,在△ABC中,O是三角形内任一点,AO、BO、CO的延长线交对边于D、E、F。求证:AE/EC+AF/FB=AO/OD。
解题思路:参考图2中燕尾定理公式,将欲证线段等式AE/EC+AF/FB=AO/OD用面积比例显示如下:
AE/EC = S△AOB/ S△BOC;
AF/FB = S△AOC/ S△BOC。
AE/EC+AF/FB=(S△AOB+ S△AOC)/ S△BOC
=(S△ABC- S△BOC)/ S△BOC。
AE/EC+AF/FB = S△ABC/ S△BOC - 1。
AO/OD=(S△AOB+ S△AOC)/S△BOC
=( S△ABC- S△BOC) /S△BOC,
AO/OD= S△ABC/ S△BOC – 1。
故AE/EC+AF/FB=AO/OD成立。